torch稀疏
警告
该 API 目前处于实验阶段,可能会在不久的将来进行更改。
Torch 支持 COO(rdinate)格式的稀疏张量,该稀疏张量可以有效地存储和处理大多数元素为零的张量。
稀疏张量表示为一对密集张量:一个值张量和一个 2D 索引张量。 可以通过提供这两个张量以及稀疏张量的大小(无法从这些张量推断出)来构造稀疏张量假设我们要定义一个稀疏张量,其入口 3 位于位置(0,2) ,位置(1、0)处的条目 4 和位置(1、2)处的条目 5。 然后我们将写:
>>> i = torch.LongTensor([[0, 1, 1],
[2, 0, 2]])
>>> v = torch.FloatTensor([3, 4, 5])
>>> torch.sparse.FloatTensor(i, v, torch.Size([2,3])).to_dense()
0 0 3
4 0 5
[torch.FloatTensor of size 2x3]
请注意,LongTensor 的输入不是索引元组的列表。 如果要以这种方式编写索引,则应在将索引传递给稀疏构造函数之前进行转置:
>>> i = torch.LongTensor([[0, 2], [1, 0], [1, 2]])
>>> v = torch.FloatTensor([3, 4, 5 ])
>>> torch.sparse.FloatTensor(i.t(), v, torch.Size([2,3])).to_dense()
0 0 3
4 0 5
[torch.FloatTensor of size 2x3]
您还可以构造混合稀疏张量,其中仅前 n 个维是稀疏的,其余维是密集的。
>>> i = torch.LongTensor([[2, 4]])
>>> v = torch.FloatTensor([[1, 3], [5, 7]])
>>> torch.sparse.FloatTensor(i, v).to_dense()
0 0
0 0
1 3
0 0
5 7
[torch.FloatTensor of size 5x2]
可以通过指定大小来构造一个空的稀疏张量:
>>> torch.sparse.FloatTensor(2, 3)
SparseFloatTensor of size 2x3 with indices:
[torch.LongTensor with no dimension]
and values:
[torch.FloatTensor with no dimension]
SparseTensor has the following invariants:
-
sparse_dim + density_dim = len(SparseTensor.shape)
-
SparseTensor._indices()。shape =(sparse_dim,nnz)
-
SparseTensor._values()。shape =(nnz,SparseTensor.shape [sparse_dim:])
由于 SparseTensor._indices()始终是 2D 张量,因此最小的 sparse_dim =1。因此,sparse_dim = 0 的 SparseTensor 的表示只是一个密集的张量。
注意
我们的稀疏张量格式允许_不分众的_稀疏张量,其中索引中可能有重复的坐标; 在这种情况下,解释是该索引处的值是所有重复值条目的总和。 张量张量允许我们更有效地实施某些运算符。
在大多数情况下,您不必担心稀疏张量是否合并,因为在合并或未合并稀疏张量的情况下,大多数操作都可以相同地工作。 但是,在两种情况下,您可能需要注意。
首先,如果您反复执行可能产生重复项的操作(例如 torch.sparse.FloatTensor.add()),则应偶尔合并稀疏张量以防止它们变得太大。
其次,某些运算符会根据是否合并而产生不同的值(例如 torch.sparse.FloatTensor._values() 和 torch.sparse.FloatTensor._indices() 以及 torch.Tensor.sparse_mask())。 这些运算符以下划线作为前缀,表示它们揭示了内部实现细节,因此应谨慎使用,因为与合并的稀疏张量一起使用的代码可能不适用于未合并的稀疏张量; 一般来说,与这些运营商合作之前,明确合并是最安全的。
例如,假设我们想通过直接在 torch.sparse.FloatTensor._values() 上进行操作来实现一个运算符。 标量乘法可以很明显地实现,因为乘法分布在加法上。 但是,平方根不能直接实现,因为sqrt(a + b) != sqrt(a) + sqrt(b)(如果给定非张量的张量,将计算出平方根)。
class torch.sparse.FloatTensor¶
add()¶
add_()¶
clone()¶
dim()¶
div()¶
div_()¶
get_device()¶
hspmm()¶
mm()¶
mul()¶
mul_()¶
narrow_copy()¶
resizeAs_()¶
size()¶
spadd()¶
spmm()¶
sspaddmm()¶
sspmm()¶
sub()¶
sub_()¶
t_()¶
to_dense()¶
transpose()¶
transpose_()¶
zero_()¶
coalesce()¶
is_coalesced()¶
_indices()¶
_values()¶
_nnz()¶
功能
torch.sparse.addmm(mat, mat1, mat2, beta=1, alpha=1)¶
该函数与 torch.addmm() 的功能完全相同,只是它支持稀疏矩阵mat1的向后功能。 mat1需要具有 <cite>sparse_dim = 2</cite> 。 请注意,mat1的梯度是合并的稀疏张量。
参数
-
垫 (tensor)–要添加的密集矩阵
-
mat1 (SparseTensor )–要相乘的稀疏矩阵
-
mat2 (tensor)–密矩阵相乘
-
beta (数字 , 可选)–
mat(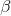 )的乘数
)的乘数 -
alpha (编号 , 可选)–
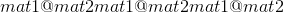 (
(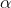 )的乘数
)的乘数
torch.sparse.mm(mat1, mat2)¶
对稀疏矩阵mat1与密集矩阵mat2进行矩阵乘法。 与 torch.mm() 相似,如果mat1是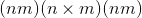 张量,
张量,mat2是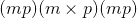 张量,则输出将是
张量,则输出将是 密集张量。
密集张量。 mat1需要具有 <cite>sparse_dim = 2</cite> 。 此功能还支持两个矩阵的向后。 请注意,mat1的梯度是合并的稀疏张量。
Parameters
-
mat1 (SparseTensor )–第一个要相乘的稀疏矩阵
-
mat2 (tensor)–要相乘的第二个密集矩阵
例:
>>> a = torch.randn(2, 3).to_sparse().requires_grad_(True)
>>> a
tensor(indices=tensor([[0, 0, 0, 1, 1, 1],
[0, 1, 2, 0, 1, 2]]),
values=tensor([ 1.5901, 0.0183, -0.6146, 1.8061, -0.0112, 0.6302]),
size=(2, 3), nnz=6, layout=torch.sparse_coo, requires_grad=True)
>>> b = torch.randn(3, 2, requires_grad=True)
>>> b
tensor([[-0.6479, 0.7874],
[-1.2056, 0.5641],
[-1.1716, -0.9923]], requires_grad=True)
>>> y = torch.sparse.mm(a, b)
>>> y
tensor([[-0.3323, 1.8723],
[-1.8951, 0.7904]], grad_fn=<SparseAddmmBackward>)
>>> y.sum().backward()
>>> a.grad
tensor(indices=tensor([[0, 0, 0, 1, 1, 1],
[0, 1, 2, 0, 1, 2]]),
values=tensor([ 0.1394, -0.6415, -2.1639, 0.1394, -0.6415, -2.1639]),
size=(2, 3), nnz=6, layout=torch.sparse_coo)
torch.sparse.sum(input, dim=None, dtype=None)¶
返回给定维度dim中 SparseTensor input每行的总和。 如果dim是尺寸列表,请缩小所有尺寸。 当对所有sparse_dim求和时,此方法返回张量而不是 SparseTensor。
压缩所有求和的dim(请参见 torch.squeeze()),从而使输出张量的尺寸比input小。
在向后期间,仅input的nnz位置处的梯度将传播回去。 注意,input的梯度是合并的。
Parameters
-
输入 (tensor)–输入 SparseTensor
-
暗淡的 (python:int 或 python:ints 的元组)–一个要减小的尺寸或尺寸列表。 默认值:减少所有暗淡。
-
dtype (
torch.dtype,可选)–返回的 Tensor 的所需数据类型。 默认值:input的 dtype。
Example:
>>> nnz = 3
>>> dims = [5, 5, 2, 3]
>>> I = torch.cat([torch.randint(0, dims[0], size=(nnz,)),
torch.randint(0, dims[1], size=(nnz,))], 0).reshape(2, nnz)
>>> V = torch.randn(nnz, dims[2], dims[3])
>>> size = torch.Size(dims)
>>> S = torch.sparse_coo_tensor(I, V, size)
>>> S
tensor(indices=tensor([[2, 0, 3],
[2, 4, 1]]),
values=tensor([[[-0.6438, -1.6467, 1.4004],
[ 0.3411, 0.0918, -0.2312]],
[[ 0.5348, 0.0634, -2.0494],
[-0.7125, -1.0646, 2.1844]],
[[ 0.1276, 0.1874, -0.6334],
[-1.9682, -0.5340, 0.7483]]]),
size=(5, 5, 2, 3), nnz=3, layout=torch.sparse_coo)
# when sum over only part of sparse_dims, return a SparseTensor
>>> torch.sparse.sum(S, [1, 3])
tensor(indices=tensor([[0, 2, 3]]),
values=tensor([[-1.4512, 0.4073],
[-0.8901, 0.2017],
[-0.3183, -1.7539]]),
size=(5, 2), nnz=3, layout=torch.sparse_coo)
# when sum over all sparse dim, return a dense Tensor
# with summed dims squeezed
>>> torch.sparse.sum(S, [0, 1, 3])
tensor([-2.6596, -1.1450])

